How To
the Secrets: A Comprehensive Guide how to breed humbug

Description
If you’ve ever wanted to know how to breed humbug, you’ve come to the perfect spot. This all-inclusive manual will teach you all you need to know to breed humbugs like a pro.
Learning the Fundamentals as a Starting Point
Before you can start breeding humbugs, you need to learn the fundamentals. Humbugs require careful preparation before being developed due to their peculiar characteristics.
The Humbug Breeding Essentials
The following are the bare minimums that must be met for successful humbug breeding:
Selecting the Right Pairing:
Pick humbugs who share characteristics for a healthy offspring.
Optimal Breeding Conditions:
Make sure the temperature, humidity, and food supply are all optimal.
Monitoring Gestation Period:
Be on the lookout for the onset of the humbug offspring’s gestation phase.
A Step-by-Step Guide to Humbug Breeding
Choosing the Right Humbug Pair
As a first step, pick a couple of humbugs that have qualities that compliment each other. This is vital in order to establish a robust and adaptable humbug lineage.
Creating the Perfect Environment
There are situations that are ideal for how to breed humbug. It’s important to keep the breeding environment at just the right temperature, humidity, and food levels for the animals.
Nurturing the Gestation Period
Keep a watchful eye on the humbug parents during the pregnancy. Prepare a safe haven for the upcoming humbug offspring by giving them extra food and attention.
The Art of Humbug Parenting
A Hands-On Approach
Hands-on humbug parenting is the finest way to take care of the kids. Create a warm and welcoming atmosphere by talking to the grumpy parents.
Ensuring Continued Success
Maintaining ideal circumstances once the kids have arrived is essential for maintaining a robust humbug community. This ensures that the humbug population will grow strong and flourish.
Conclusion
In conclusion, humbug breeding is an art that takes precision and attention. If you follow the steps in this manual, you should have no trouble raising humbugs like a pro in no time. Keep in mind that each action is vital, and the final product is well worth the effort.
Start your humbug breeding adventure today and see firsthand how amazing it is to see a humbug population grow. Breed successfully!
Entertainment
The Mesmerizing World of Slime
How To
Taser High Voltage: Understanding its Mechanism and Impact

Introduction
The Taser, an acronym for “Thomas A. Swift’s Electric Rifle,” has become synonymous with non-lethal law enforcement. One of its key components is high voltage, a critical factor influencing its effectiveness and safety. This article delves into the specifics of Taser high voltage, its function, impact, and safety considerations.
What is a Taser?
Taser devices are electroshock weapons that use electrical currents to disrupt voluntary control of muscles, causing neuromuscular incapacitation. They’re widely employed by law enforcement to subdue suspects without causing significant harm.
Components of a Taser
- High Voltage Module:
- The heart of a Taser is its high voltage module, generating electrical pulses.
- Voltage typically ranges from 50,000 to 150,000 volts in most commercial Tasers.
- Despite the high voltage, the amperage—the actual current—is low, reducing the risk of causing lethal harm.
- Power Source:
- Tasers use lithium batteries or replaceable cartridges to power the high voltage module.
How Does Taser High Voltage Work?
- Electrostatic Discharge:
- When activated, the Taser releases two probes connected by wires.
- These probes deliver high-voltage, low-current electrical pulses, creating an arc of electricity.
- Neuromuscular Incapacitation:
- The electrical pulses disrupt the body’s normal electrical signals, causing involuntary muscle contractions.
- This disrupts neuromuscular control, leading to temporary incapacitation.
Impact on the Human Body
- Pain and Discomfort:
- Taser activation causes severe pain and discomfort due to intense muscle contractions.
- However, once the Taser is deactivated, the effects are usually short-lived.
- Potential Risks:
- While Tasers are generally considered non-lethal, there have been instances of complications, especially in individuals with pre-existing heart conditions.
- Medical experts advise caution when using Tasers, particularly on vulnerable populations.
Safety Considerations and Regulations
- Law Enforcement Guidelines:
- Law enforcement agencies often have strict protocols on Taser usage.
- Guidelines emphasize using Tasers as a last resort and avoiding prolonged or repeated shocks.
- Training and Education:
- Proper training on Taser use is crucial for law enforcement officers to minimize risks.
- This includes understanding the physiological effects and recognizing situations where Taser use is appropriate.
Misconceptions Surrounding Taser High Voltage
- Lethality vs. Non-Lethality:
- Despite high voltage, Tasers are designed to be non-lethal due to their low amperage.
- However, misuse or application on vulnerable areas can lead to adverse outcomes.
- Long-Term Health Effects:
- Studies on the long-term effects of Taser high voltage on human health are inconclusive.
- Continued research is necessary to understand any potential long-term implications.
Conclusion
Taser high voltage plays a pivotal role in the functioning of these electroshock weapons, offering law enforcement a non-lethal means of incapacitating suspects. While generally considered safe when used correctly, caution and adherence to guidelines are essential to mitigate potential risks. Understanding the mechanism and impact of Taser high voltage is crucial for ensuring its responsible and effective usage in law enforcement scenarios.
FAQS:
How To
Unveiling the Mystery of 6x – 6:
-

 Technology7 months ago
Technology7 months agoKooraLive English: Guide to Live Sports Streaming
-
 Technology7 months ago
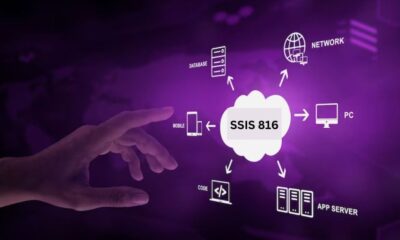
Technology7 months agoSSIS 816 Revolutionizing Data Integration
-
 Health7 months ago
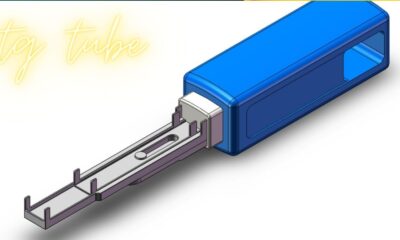
Health7 months agoOptimizing Health: The Comprehensive Guide to TG Tubes
-

 Lifestyle6 months ago
Lifestyle6 months agothe Charm of Villages: Decoding the Loofa Code
-

 Entertainment6 months ago
Entertainment6 months agothe Mystery: packgod face reveal
-

 Business4 months ago
Business4 months agoSimplifying Work Life: NetchexOnline Employee Login
-

 Technology7 months ago
Technology7 months agoPotential of Pixwox: Your Guide to Superior Visual Content
-

 Technology7 months ago
Technology7 months agoThe Power of Innocams

